[백준] 17472 다리 만들기 2 - 자바

https://www.acmicpc.net/problem/17472

17472번: 다리 만들기 2

문제 풀이

그래프에 관한 많은 알고리즘을 적용된 문제로 필자는 bfs, dfs, kruskal 알고리즘을 적용하였다.

기존 MST 문제인 1774 우주신과의 교감 or 4386 별자리 만들기 문제처럼 직접 노드를 구성하여 해당 노드와 연결되는 모든 간선을 구하고 이를 활용하여 MST 구하는 과정은 비슷하다.

다만 이 문제는 각 노드가 점(x, y)가 아닌 점들로 이루어진 평면좌표라는 것이다. 따라서 노드를 이 평면좌표를 활용하여 구성하는 것이 핵심이다.

 

init islandList - bfs

먼저 입력으로 주어지는 보드를 저장하고 1로 이루어진 섬들에 대해 1, 2, 3, --- 으로 섬의 넘버를 부여한다. 이때 해당 섬의 좌표들은 각 섬이 가지는 넘버링의 수로 값을 수정한다.

// init islandList
int numbering = 1;
visit = new boolean[N][M];
for (int i = 0; i < N; i++) {
    for (int j = 0; j < M; j++) {
        if (board[i][j] == 1 && !visit[i][j]) {
            insertIslandList(i, j, numbering);
            numbering++;
        }
    }
}

static void insertIslandList(int i, int j, int numbering) {
    Island island = new Island(numbering);
    List<Point> area = new ArrayList<>();
    // init area
    bfs(i, j, area, numbering);
    island.setArea(area);

    islandList.add(island);
}

static void bfs(int i, int j, List<Point> area, int numbering) {
    board[i][j] = numbering;
    visit[i][j] = true;
    area.add(new Point(i, j));

    Queue<Point> q = new LinkedList<>();
    q.offer(new Point(i, j));
    while (!q.isEmpty()) {
        Point now = q.poll();
        for (int k = 0; k < 4; k++) {
            int nx = now.x + dx[k];
            int ny = now.y + dy[k];

            if (outOfBoardRange(nx, ny) || visit[nx][ny] || board[nx][ny] == 0) {
                continue;
            }
            board[nx][ny] = numbering;
            area.add(new Point(nx, ny));

            visit[nx][ny] = true;
            q.offer(new Point(nx, ny));
        }
    }
}

class Point {
    int x;
    int y;

    public Point(int x, int y) {
        this.x = x;
        this.y = y;
    }
}

class Island {
    int idx;
    List<Point> area;

    public Island(int idx) {
        this.idx = idx;
    }

    public List<Point> getArea() {
        return area;
    }

    public void setArea(List<Point> area) {
        this.area = area;
    }
}

예제 입력1 번을 예시로 위 함수들을 거쳤을 때 보드와 islandList는 다음처럼 값이 저장된다.

 

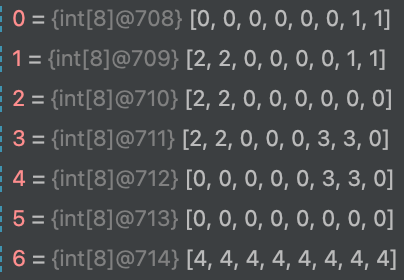
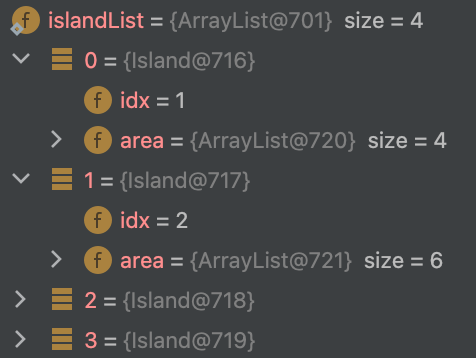
init bridgeList - dfs

bfs를 통해서도 구할 수 있지만 그러면 Point에 int depth를 추가해야 한다. 사실 수정하기 귀찮았다.

// init bridgeList
bridgeList = new ArrayList<>();
for (int i = 0; i < islandList.size(); i++) {
    Island island = islandList.get(i);
    List<Point> area = island.getArea();

    for (int j = 0; j < area.size(); j++) {
        Point point = area.get(j);

        for (int dir = 0; dir < 4; dir++) {
            findBridge(island.idx, point.x, point.y, dir, -1);
        }
    }
}

static void findBridge(int idx, int x, int y, int dir, int distance) {
    if(board[x][y] != 0 && board[x][y] != idx) { //다른 섬을 만남
        if(distance >= 2) bridgeList.add(new Bridge(idx, board[x][y], distance));
        return;
    }

    int nx = x + dx[dir];
    int ny = y + dy[dir];
    if (outOfBoardRange(nx, ny) || board[nx][ny] == idx) {
        return;
    }

    findBridge(idx, nx, ny, dir, distance + 1);
}

 

여기까지는 기본적인 그래프탐색을 적용하여 각 섬들을 노드로 변환하고 각 노드(섬)에서 연결될 수 있는 간선들을 모두 list에 저장하였다.

Kruskal - MST 구하기

bridgeList.sort((b1, b2) -> b1.distance - b2.distance);
System.out.println(kruskal());

Kruskal을 적용하기 위해선 기본적으로 간선의 비용이 오름차순으로 정렬되어 있어야 한다.

static int[] parent;
static int kruskal() {
    int size = islandList.size();
    parent = new int[size + 1];
    for (int i = 1; i < size+1; i++) {
        parent[i] = i;
    }

    int mstEdgeCnt = 0;
    int weight = 0;
    for (int i = 0; i < bridgeList.size(); i++) {
        Bridge bridge = bridgeList.get(i);
        int idx1 = bridge.idx1;
        int idx2 = bridge.idx2;

        if (union(idx1, idx2)) {
            mstEdgeCnt++;
            weight += bridge.distance;

            // MST의 간선 개수 == 노드 개수 - 1
            // 즉, 모든 섬을 이어주는 다리의 개수 = 섬의 개수 - - 1
            if (mstEdgeCnt == islandList.size() - 1) {
                return weight;
            }
        }
    }
    return -1;
}
static boolean union(int idx1, int idx2) {
    int root1 = find(idx1);
    int root2 = find(idx2);

    if (root1 == root2) {
        return false;
    }

    parent[root2] = root1;
    return true;
}

static int find(int n) {
    if (parent[n] != n) {
        parent[n] = find(parent[n]);
    }
    return parent[n];
}

class Bridge {
    int idx1;
    int idx2;
    int distance;

    public Bridge(int idx1, int idx2, int distance) {
        this.idx1 = idx1;
        this.idx2 = idx2;
        this.distance = distance;
    }
}

이전 union-find 문제를 풀어봤다면 kruskal도 크게 어렵지 않을 것이다.

 

 

코드

package 백준;

import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;
import java.util.*;

public class b17472 {
    static int N, M;
    static int[][] board;
    static List<Island> islandList;
    static boolean[][] visit;
    static List<Bridge> bridgeList;

    public static void main(String[] args) throws IOException {
        BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
        StringTokenizer st = new StringTokenizer(br.readLine());
        N = Integer.parseInt(st.nextToken());
        M = Integer.parseInt(st.nextToken());

        // init board
        islandList = new ArrayList<>();
        board = new int[N][M];
        for (int i = 0; i < N; i++) {
            board[i] = Arrays.stream(br.readLine().split(" ")).mapToInt(Integer::parseInt).toArray();
        }

        // init islandList
        int numbering = 1;
        visit = new boolean[N][M];
        for (int i = 0; i < N; i++) {
            for (int j = 0; j < M; j++) {
                if (board[i][j] == 1 && !visit[i][j]) {
                    insertIslandList(i, j, numbering);
                    numbering++;
                }
            }
        }

        // init bridgeList
        bridgeList = new ArrayList<>();
        for (int i = 0; i < islandList.size(); i++) {
            Island island = islandList.get(i);
            List<Point> area = island.getArea();

            for (int j = 0; j < area.size(); j++) {
                Point point = area.get(j);

                for (int dir = 0; dir < 4; dir++) {
                    findBridge(island.idx, point.x, point.y, dir, -1);
                }
            }
        }

        bridgeList.sort((b1, b2) -> b1.distance - b2.distance);
        System.out.println(kruskal());
    }

    static int[] parent;
    static int kruskal() {
        int size = islandList.size();
        parent = new int[size + 1];
        for (int i = 1; i < size+1; i++) {
            parent[i] = i;
        }

        int mstEdgeCnt = 0;
        int weight = 0;
        for (int i = 0; i < bridgeList.size(); i++) {
            Bridge bridge = bridgeList.get(i);
            int idx1 = bridge.idx1;
            int idx2 = bridge.idx2;

            if (union(idx1, idx2)) {
                mstEdgeCnt++;
                weight += bridge.distance;

                // MST의 간선 개수 == 노드 개수 - 1
                // 즉, 모든 섬을 이어주는 다리의 개수 = 섬의 개수 - - 1
                if (mstEdgeCnt == islandList.size() - 1) {
                    return weight;
                }
            }
        }
        return -1;
    }
    static boolean union(int idx1, int idx2) {
        int root1 = find(idx1);
        int root2 = find(idx2);

        if (root1 == root2) {
            return false;
        }

        parent[root2] = root1;
        return true;
    }

    static int find(int n) {
        if (parent[n] != n) {
            parent[n] = find(parent[n]);
        }
        return parent[n];
    }


    static void findBridge(int idx, int x, int y, int dir, int distance) {
        if(board[x][y] != 0 && board[x][y] != idx) { //다른 섬을 만남
            if(distance >= 2) bridgeList.add(new Bridge(idx, board[x][y], distance));
            return;
        }

        int nx = x + dx[dir];
        int ny = y + dy[dir];
        if (outOfBoardRange(nx, ny) || board[nx][ny] == idx) {
            return;
        }

        findBridge(idx, nx, ny, dir, distance + 1);
    }

    static void insertIslandList(int i, int j, int numbering) {
        Island island = new Island(numbering);
        List<Point> area = new ArrayList<>();
        // init area
        bfs(i, j, area, numbering);
        island.setArea(area);

        islandList.add(island);
    }

    static int dx[] = {-1, 1, 0, 0};
    static int dy[] = {0, 0, -1, 1};

    static void bfs(int i, int j, List<Point> area, int numbering) {
        board[i][j] = numbering;
        visit[i][j] = true;
        area.add(new Point(i, j));

        Queue<Point> q = new LinkedList<>();
        q.offer(new Point(i, j));
        while (!q.isEmpty()) {
            Point now = q.poll();
            for (int k = 0; k < 4; k++) {
                int nx = now.x + dx[k];
                int ny = now.y + dy[k];

                if (outOfBoardRange(nx, ny) || visit[nx][ny] || board[nx][ny] == 0) {
                    continue;
                }
                board[nx][ny] = numbering;
                area.add(new Point(nx, ny));

                visit[nx][ny] = true;
                q.offer(new Point(nx, ny));
            }
        }
    }

    static boolean outOfBoardRange(int nx, int ny) {
        if (nx < 0 || ny < 0 || nx >= N || ny >= M) {
            return true;
        }
        return false;
    }
}

class Point {
    int x;
    int y;

    public Point(int x, int y) {
        this.x = x;
        this.y = y;
    }
}

class Island {
    int idx;
    List<Point> area;

    public Island(int idx) {
        this.idx = idx;
    }

    public List<Point> getArea() {
        return area;
    }

    public void setArea(List<Point> area) {
        this.area = area;
    }
}

class Bridge {
    int idx1;
    int idx2;
    int distance;

    public Bridge(int idx1, int idx2, int distance) {
        this.idx1 = idx1;
        this.idx2 = idx2;
        this.distance = distance;
    }
}

느낀점

기본적인 그래프 탐색과 MST를 구하는 과정을 알고 있었다 하더라도 평면좌표를 노드로 관리해야 하는 것에 접근하지 못했다면 풀기 어려운 문제가 아니였을까 싶다.